Chapter 11 – Training Deep Neural Networks
This notebook contains all the sample code and solutions to the exercises in chapter 11.
 Run in Google Colab Run in Google Colab
|
Setup
First, let’s import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures. We also check that Python 3.5 or later is installed (although Python 2.x may work, it is deprecated so we strongly recommend you use Python 3 instead), as well as Scikit-Learn ≥0.20 and TensorFlow ≥2.0.
# Python ≥3.5 is required
import sys
assert sys.version_info >= (3, 5)
# Scikit-Learn ≥0.20 is required
import sklearn
assert sklearn.__version__ >= "0.20"
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
# TensorFlow ≥2.0 is required
import tensorflow as tf
from tensorflow import keras
assert tf.__version__ >= "2.0"
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "deep"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
Vanishing/Exploding Gradients Problem
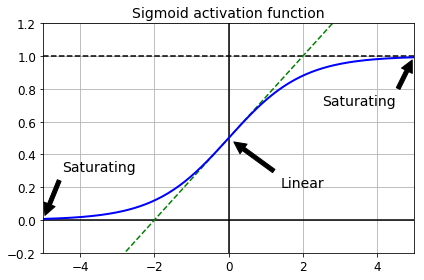
def logit(z):
return 1 / (1 + np.exp(-z))
z = np.linspace(-5, 5, 200)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([-5, 5], [1, 1], 'k--')
plt.plot([0, 0], [-0.2, 1.2], 'k-')
plt.plot([-5, 5], [-3/4, 7/4], 'g--')
plt.plot(z, logit(z), "b-", linewidth=2)
props = dict(facecolor='black', shrink=0.1)
plt.annotate('Saturating', xytext=(3.5, 0.7), xy=(5, 1), arrowprops=props, fontsize=14, ha="center")
plt.annotate('Saturating', xytext=(-3.5, 0.3), xy=(-5, 0), arrowprops=props, fontsize=14, ha="center")
plt.annotate('Linear', xytext=(2, 0.2), xy=(0, 0.5), arrowprops=props, fontsize=14, ha="center")
plt.grid(True)
plt.title("Sigmoid activation function", fontsize=14)
plt.axis([-5, 5, -0.2, 1.2])
save_fig("sigmoid_saturation_plot")
plt.show()
Xavier and He Initialization
[name for name in dir(keras.initializers) if not name.startswith("_")]
keras.layers.Dense(10, activation="relu", kernel_initializer="he_normal")
init = keras.initializers.VarianceScaling(scale=2., mode='fan_avg',
distribution='uniform')
keras.layers.Dense(10, activation="relu", kernel_initializer=init)
Nonsaturating Activation Functions
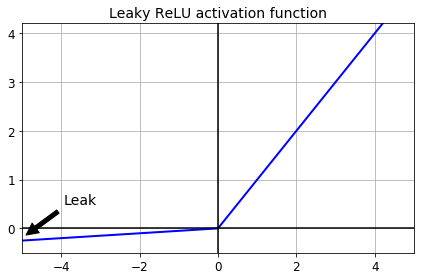
Leaky ReLU
def leaky_relu(z, alpha=0.01):
return np.maximum(alpha*z, z)
plt.plot(z, leaky_relu(z, 0.05), "b-", linewidth=2)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([0, 0], [-0.5, 4.2], 'k-')
plt.grid(True)
props = dict(facecolor='black', shrink=0.1)
plt.annotate('Leak', xytext=(-3.5, 0.5), xy=(-5, -0.2), arrowprops=props, fontsize=14, ha="center")
plt.title("Leaky ReLU activation function", fontsize=14)
plt.axis([-5, 5, -0.5, 4.2])
save_fig("leaky_relu_plot")
plt.show()
[m for m in dir(keras.activations) if not m.startswith("_")]
[m for m in dir(keras.layers) if "relu" in m.lower()]
Let’s train a neural network on Fashion MNIST using the Leaky ReLU:
(X_train_full, y_train_full), (X_test, y_test) = keras.datasets.fashion_mnist.load_data()
X_train_full = X_train_full / 255.0
X_test = X_test / 255.0
X_valid, X_train = X_train_full[:5000], X_train_full[5000:]
y_valid, y_train = y_train_full[:5000], y_train_full[5000:]
tf.random.set_seed(42)
np.random.seed(42)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, kernel_initializer="he_normal"),
keras.layers.LeakyReLU(),
keras.layers.Dense(100, kernel_initializer="he_normal"),
keras.layers.LeakyReLU(),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid))
Now let’s try PReLU:
tf.random.set_seed(42)
np.random.seed(42)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, kernel_initializer="he_normal"),
keras.layers.PReLU(),
keras.layers.Dense(100, kernel_initializer="he_normal"),
keras.layers.PReLU(),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid))
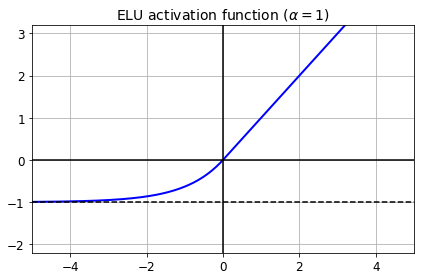
ELU
def elu(z, alpha=1):
return np.where(z < 0, alpha * (np.exp(z) - 1), z)
plt.plot(z, elu(z), "b-", linewidth=2)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([-5, 5], [-1, -1], 'k--')
plt.plot([0, 0], [-2.2, 3.2], 'k-')
plt.grid(True)
plt.title(r"ELU activation function ($\alpha=1$)", fontsize=14)
plt.axis([-5, 5, -2.2, 3.2])
save_fig("elu_plot")
plt.show()
Implementing ELU in TensorFlow is trivial, just specify the activation function when building each layer:
keras.layers.Dense(10, activation="elu")
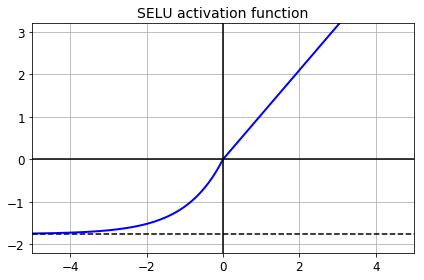
SELU
This activation function was proposed in this great paper by Günter Klambauer, Thomas Unterthiner and Andreas Mayr, published in June 2017. During training, a neural network composed exclusively of a stack of dense layers using the SELU activation function and LeCun initialization will self-normalize: the output of each layer will tend to preserve the same mean and variance during training, which solves the vanishing/exploding gradients problem. As a result, this activation function outperforms the other activation functions very significantly for such neural nets, so you should really try it out. Unfortunately, the self-normalizing property of the SELU activation function is easily broken: you cannot use ℓ1 or ℓ2 regularization, regular dropout, max-norm, skip connections or other non-sequential topologies (so recurrent neural networks won’t self-normalize). However, in practice it works quite well with sequential CNNs. If you break self-normalization, SELU will not necessarily outperform other activation functions.
from scipy.special import erfc
# alpha and scale to self normalize with mean 0 and standard deviation 1
# (see equation 14 in the paper):
alpha_0_1 = -np.sqrt(2 / np.pi) / (erfc(1/np.sqrt(2)) * np.exp(1/2) - 1)
scale_0_1 = (1 - erfc(1 / np.sqrt(2)) * np.sqrt(np.e)) * np.sqrt(2 * np.pi) * (2 * erfc(np.sqrt(2))*np.e**2 + np.pi*erfc(1/np.sqrt(2))**2*np.e - 2*(2+np.pi)*erfc(1/np.sqrt(2))*np.sqrt(np.e)+np.pi+2)**(-1/2)
def selu(z, scale=scale_0_1, alpha=alpha_0_1):
return scale * elu(z, alpha)
plt.plot(z, selu(z), "b-", linewidth=2)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([-5, 5], [-1.758, -1.758], 'k--')
plt.plot([0, 0], [-2.2, 3.2], 'k-')
plt.grid(True)
plt.title("SELU activation function", fontsize=14)
plt.axis([-5, 5, -2.2, 3.2])
save_fig("selu_plot")
plt.show()
By default, the SELU hyperparameters (scale and alpha) are tuned in such a way that the mean output of each neuron remains close to 0, and the standard deviation remains close to 1 (assuming the inputs are standardized with mean 0 and standard deviation 1 too). Using this activation function, even a 1,000 layer deep neural network preserves roughly mean 0 and standard deviation 1 across all layers, avoiding the exploding/vanishing gradients problem:
np.random.seed(42)
Z = np.random.normal(size=(500, 100)) # standardized inputs
for layer in range(1000):
W = np.random.normal(size=(100, 100), scale=np.sqrt(1 / 100)) # LeCun initialization
Z = selu(np.dot(Z, W))
means = np.mean(Z, axis=0).mean()
stds = np.std(Z, axis=0).mean()
if layer % 100 == 0:
print("Layer {}: mean {:.2f}, std deviation {:.2f}".format(layer, means, stds))
Using SELU is easy:
keras.layers.Dense(10, activation="selu",
kernel_initializer="lecun_normal")
Let’s create a neural net for Fashion MNIST with 100 hidden layers, using the SELU activation function:
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28, 28]))
model.add(keras.layers.Dense(300, activation="selu",
kernel_initializer="lecun_normal"))
for layer in range(99):
model.add(keras.layers.Dense(100, activation="selu",
kernel_initializer="lecun_normal"))
model.add(keras.layers.Dense(10, activation="softmax"))
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
Now let’s train it. Do not forget to scale the inputs to mean 0 and standard deviation 1:
pixel_means = X_train.mean(axis=0, keepdims=True)
pixel_stds = X_train.std(axis=0, keepdims=True)
X_train_scaled = (X_train - pixel_means) / pixel_stds
X_valid_scaled = (X_valid - pixel_means) / pixel_stds
X_test_scaled = (X_test - pixel_means) / pixel_stds
history = model.fit(X_train_scaled, y_train, epochs=5,
validation_data=(X_valid_scaled, y_valid))
Now look at what happens if we try to use the ReLU activation function instead:
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28, 28]))
model.add(keras.layers.Dense(300, activation="relu", kernel_initializer="he_normal"))
for layer in range(99):
model.add(keras.layers.Dense(100, activation="relu", kernel_initializer="he_normal"))
model.add(keras.layers.Dense(10, activation="softmax"))
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model.fit(X_train_scaled, y_train, epochs=5,
validation_data=(X_valid_scaled, y_valid))
Not great at all, we suffered from the vanishing/exploding gradients problem.
Batch Normalization
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.BatchNormalization(),
keras.layers.Dense(300, activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.Dense(100, activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.Dense(10, activation="softmax")
])
model.summary()
bn1 = model.layers[1]
[(var.name, var.trainable) for var in bn1.variables]
bn1.updates
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid))
Sometimes applying BN before the activation function works better (there’s a debate on this topic). Moreover, the layer before a BatchNormalization layer does not need to have bias terms, since the BatchNormalization layer some as well, it would be a waste of parameters, so you can set use_bias=False when creating those layers:
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.BatchNormalization(),
keras.layers.Dense(300, use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation("relu"),
keras.layers.Dense(100, use_bias=False),
keras.layers.Activation("relu"),
keras.layers.BatchNormalization(),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid))
Gradient Clipping
All Keras optimizers accept clipnorm or clipvalue arguments:
optimizer = keras.optimizers.SGD(clipvalue=1.0)
optimizer = keras.optimizers.SGD(clipnorm=1.0)
Reusing Pretrained Layers
Reusing a Keras model
Let’s split the fashion MNIST training set in two:
X_train_A: all images of all items except for sandals and shirts (classes 5 and 6).X_train_B: a much smaller training set of just the first 200 images of sandals or shirts.
The validation set and the test set are also split this way, but without restricting the number of images.
We will train a model on set A (classification task with 8 classes), and try to reuse it to tackle set B (binary classification). We hope to transfer a little bit of knowledge from task A to task B, since classes in set A (sneakers, ankle boots, coats, t-shirts, etc.) are somewhat similar to classes in set B (sandals and shirts). However, since we are using Dense layers, only patterns that occur at the same location can be reused (in contrast, convolutional layers will transfer much better, since learned patterns can be detected anywhere on the image, as we will see in the CNN chapter).
def split_dataset(X, y):
y_5_or_6 = (y == 5) | (y == 6) # sandals or shirts
y_A = y[~y_5_or_6]
y_A[y_A > 6] -= 2 # class indices 7, 8, 9 should be moved to 5, 6, 7
y_B = (y[y_5_or_6] == 6).astype(np.float32) # binary classification task: is it a shirt (class 6)?
return ((X[~y_5_or_6], y_A),
(X[y_5_or_6], y_B))
(X_train_A, y_train_A), (X_train_B, y_train_B) = split_dataset(X_train, y_train)
(X_valid_A, y_valid_A), (X_valid_B, y_valid_B) = split_dataset(X_valid, y_valid)
(X_test_A, y_test_A), (X_test_B, y_test_B) = split_dataset(X_test, y_test)
X_train_B = X_train_B[:200]
y_train_B = y_train_B[:200]
X_train_A.shape
X_train_B.shape
y_train_A[:30]
y_train_B[:30]
tf.random.set_seed(42)
np.random.seed(42)
model_A = keras.models.Sequential()
model_A.add(keras.layers.Flatten(input_shape=[28, 28]))
for n_hidden in (300, 100, 50, 50, 50):
model_A.add(keras.layers.Dense(n_hidden, activation="selu"))
model_A.add(keras.layers.Dense(8, activation="softmax"))
model_A.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model_A.fit(X_train_A, y_train_A, epochs=20,
validation_data=(X_valid_A, y_valid_A))
model_A.save("my_model_A.h5")
model_B = keras.models.Sequential()
model_B.add(keras.layers.Flatten(input_shape=[28, 28]))
for n_hidden in (300, 100, 50, 50, 50):
model_B.add(keras.layers.Dense(n_hidden, activation="selu"))
model_B.add(keras.layers.Dense(1, activation="sigmoid"))
model_B.compile(loss="binary_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model_B.fit(X_train_B, y_train_B, epochs=20,
validation_data=(X_valid_B, y_valid_B))
model.summary()
model_A = keras.models.load_model("my_model_A.h5")
model_B_on_A = keras.models.Sequential(model_A.layers[:-1])
model_B_on_A.add(keras.layers.Dense(1, activation="sigmoid"))
model_A_clone = keras.models.clone_model(model_A)
model_A_clone.set_weights(model_A.get_weights())
for layer in model_B_on_A.layers[:-1]:
layer.trainable = False
model_B_on_A.compile(loss="binary_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model_B_on_A.fit(X_train_B, y_train_B, epochs=4,
validation_data=(X_valid_B, y_valid_B))
for layer in model_B_on_A.layers[:-1]:
layer.trainable = True
model_B_on_A.compile(loss="binary_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model_B_on_A.fit(X_train_B, y_train_B, epochs=16,
validation_data=(X_valid_B, y_valid_B))
So, what’s the final verdict?
model_B.evaluate(X_test_B, y_test_B)
model_B_on_A.evaluate(X_test_B, y_test_B)
Great! We got quite a bit of transfer: the error rate dropped by a factor of almost 4!
(100 - 97.05) / (100 - 99.25)
Faster Optimizers
Momentum optimization
optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9)
Nesterov Accelerated Gradient
optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9, nesterov=True)
AdaGrad
optimizer = keras.optimizers.Adagrad(lr=0.001)
RMSProp
optimizer = keras.optimizers.RMSprop(lr=0.001, rho=0.9)
Adam Optimization
optimizer = keras.optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.999)
Adamax Optimization
optimizer = keras.optimizers.Adamax(lr=0.001, beta_1=0.9, beta_2=0.999)
Nadam Optimization
optimizer = keras.optimizers.Nadam(lr=0.001, beta_1=0.9, beta_2=0.999)
Learning Rate Scheduling
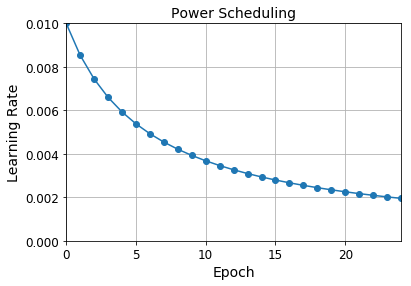
Power Scheduling
lr = lr0 / (1 + steps / s)**c
- Keras uses
c=1ands = 1 / decay
optimizer = keras.optimizers.SGD(lr=0.01, decay=1e-4)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer, metrics=["accuracy"])
n_epochs = 25
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid))
learning_rate = 0.01
decay = 1e-4
batch_size = 32
n_steps_per_epoch = len(X_train) // batch_size
epochs = np.arange(n_epochs)
lrs = learning_rate / (1 + decay * epochs * n_steps_per_epoch)
plt.plot(epochs, lrs, "o-")
plt.axis([0, n_epochs - 1, 0, 0.01])
plt.xlabel("Epoch")
plt.ylabel("Learning Rate")
plt.title("Power Scheduling", fontsize=14)
plt.grid(True)
plt.show()
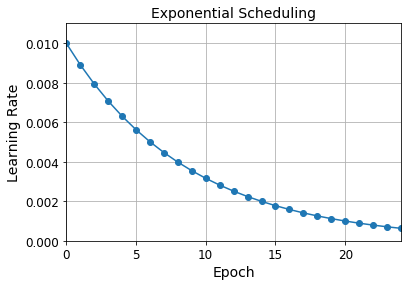
Exponential Scheduling
lr = lr0 * 0.1**(epoch / s)
def exponential_decay_fn(epoch):
return 0.01 * 0.1**(epoch / 20)
def exponential_decay(lr0, s):
def exponential_decay_fn(epoch):
return lr0 * 0.1**(epoch / s)
return exponential_decay_fn
exponential_decay_fn = exponential_decay(lr0=0.01, s=20)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy", optimizer="nadam", metrics=["accuracy"])
n_epochs = 25
lr_scheduler = keras.callbacks.LearningRateScheduler(exponential_decay_fn)
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid),
callbacks=[lr_scheduler])
plt.plot(history.epoch, history.history["lr"], "o-")
plt.axis([0, n_epochs - 1, 0, 0.011])
plt.xlabel("Epoch")
plt.ylabel("Learning Rate")
plt.title("Exponential Scheduling", fontsize=14)
plt.grid(True)
plt.show()
The schedule function can take the current learning rate as a second argument:
def exponential_decay_fn(epoch, lr):
return lr * 0.1**(1 / 20)
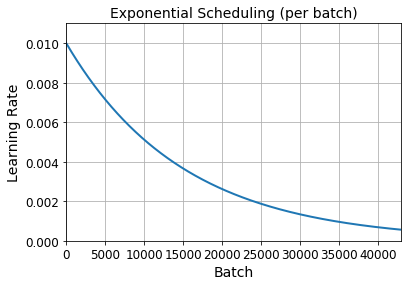
If you want to update the learning rate at each iteration rather than at each epoch, you must write your own callback class:
K = keras.backend
class ExponentialDecay(keras.callbacks.Callback):
def __init__(self, s=40000):
super().__init__()
self.s = s
def on_batch_begin(self, batch, logs=None):
# Note: the `batch` argument is reset at each epoch
lr = K.get_value(self.model.optimizer.lr)
K.set_value(self.model.optimizer.lr, lr * 0.1**(1 / s))
def on_epoch_end(self, epoch, logs=None):
logs = logs or {}
logs['lr'] = K.get_value(self.model.optimizer.lr)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(10, activation="softmax")
])
lr0 = 0.01
optimizer = keras.optimizers.Nadam(lr=lr0)
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer, metrics=["accuracy"])
n_epochs = 25
s = 20 * len(X_train) // 32 # number of steps in 20 epochs (batch size = 32)
exp_decay = ExponentialDecay(s)
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid),
callbacks=[exp_decay])
n_steps = n_epochs * len(X_train) // 32
steps = np.arange(n_steps)
lrs = lr0 * 0.1**(steps / s)
plt.plot(steps, lrs, "-", linewidth=2)
plt.axis([0, n_steps - 1, 0, lr0 * 1.1])
plt.xlabel("Batch")
plt.ylabel("Learning Rate")
plt.title("Exponential Scheduling (per batch)", fontsize=14)
plt.grid(True)
plt.show()
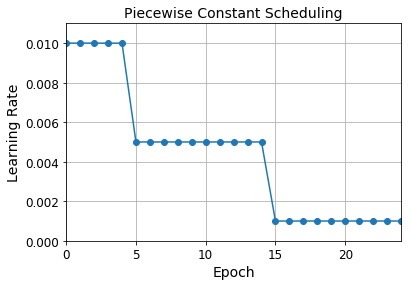
Piecewise Constant Scheduling
def piecewise_constant_fn(epoch):
if epoch < 5:
return 0.01
elif epoch < 15:
return 0.005
else:
return 0.001
def piecewise_constant(boundaries, values):
boundaries = np.array([0] + boundaries)
values = np.array(values)
def piecewise_constant_fn(epoch):
return values[np.argmax(boundaries > epoch) - 1]
return piecewise_constant_fn
piecewise_constant_fn = piecewise_constant([5, 15], [0.01, 0.005, 0.001])
lr_scheduler = keras.callbacks.LearningRateScheduler(piecewise_constant_fn)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy", optimizer="nadam", metrics=["accuracy"])
n_epochs = 25
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid),
callbacks=[lr_scheduler])
plt.plot(history.epoch, [piecewise_constant_fn(epoch) for epoch in history.epoch], "o-")
plt.axis([0, n_epochs - 1, 0, 0.011])
plt.xlabel("Epoch")
plt.ylabel("Learning Rate")
plt.title("Piecewise Constant Scheduling", fontsize=14)
plt.grid(True)
plt.show()
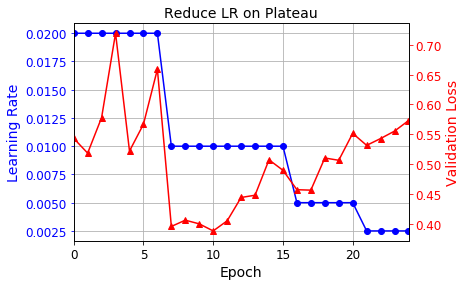
Performance Scheduling
tf.random.set_seed(42)
np.random.seed(42)
lr_scheduler = keras.callbacks.ReduceLROnPlateau(factor=0.5, patience=5)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(10, activation="softmax")
])
optimizer = keras.optimizers.SGD(lr=0.02, momentum=0.9)
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer, metrics=["accuracy"])
n_epochs = 25
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid),
callbacks=[lr_scheduler])
plt.plot(history.epoch, history.history["lr"], "bo-")
plt.xlabel("Epoch")
plt.ylabel("Learning Rate", color='b')
plt.tick_params('y', colors='b')
plt.gca().set_xlim(0, n_epochs - 1)
plt.grid(True)
ax2 = plt.gca().twinx()
ax2.plot(history.epoch, history.history["val_loss"], "r^-")
ax2.set_ylabel('Validation Loss', color='r')
ax2.tick_params('y', colors='r')
plt.title("Reduce LR on Plateau", fontsize=14)
plt.show()
tf.keras schedulers
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(10, activation="softmax")
])
s = 20 * len(X_train) // 32 # number of steps in 20 epochs (batch size = 32)
learning_rate = keras.optimizers.schedules.ExponentialDecay(0.01, s, 0.1)
optimizer = keras.optimizers.SGD(learning_rate)
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer, metrics=["accuracy"])
n_epochs = 25
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid))
For piecewise constant scheduling, try this:
learning_rate = keras.optimizers.schedules.PiecewiseConstantDecay(
boundaries=[5. * n_steps_per_epoch, 15. * n_steps_per_epoch],
values=[0.01, 0.005, 0.001])
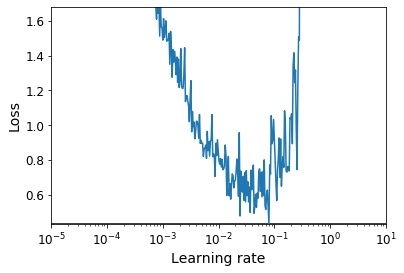
1Cycle scheduling
K = keras.backend
class ExponentialLearningRate(keras.callbacks.Callback):
def __init__(self, factor):
self.factor = factor
self.rates = []
self.losses = []
def on_batch_end(self, batch, logs):
self.rates.append(K.get_value(self.model.optimizer.lr))
self.losses.append(logs["loss"])
K.set_value(self.model.optimizer.lr, self.model.optimizer.lr * self.factor)
def find_learning_rate(model, X, y, epochs=1, batch_size=32, min_rate=10**-5, max_rate=10):
init_weights = model.get_weights()
iterations = len(X) // batch_size * epochs
factor = np.exp(np.log(max_rate / min_rate) / iterations)
init_lr = K.get_value(model.optimizer.lr)
K.set_value(model.optimizer.lr, min_rate)
exp_lr = ExponentialLearningRate(factor)
history = model.fit(X, y, epochs=epochs, batch_size=batch_size,
callbacks=[exp_lr])
K.set_value(model.optimizer.lr, init_lr)
model.set_weights(init_weights)
return exp_lr.rates, exp_lr.losses
def plot_lr_vs_loss(rates, losses):
plt.plot(rates, losses)
plt.gca().set_xscale('log')
plt.hlines(min(losses), min(rates), max(rates))
plt.axis([min(rates), max(rates), min(losses), (losses[0] + min(losses)) / 2])
plt.xlabel("Learning rate")
plt.ylabel("Loss")
tf.random.set_seed(42)
np.random.seed(42)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
batch_size = 128
rates, losses = find_learning_rate(model, X_train_scaled, y_train, epochs=1, batch_size=batch_size)
plot_lr_vs_loss(rates, losses)
class OneCycleScheduler(keras.callbacks.Callback):
def __init__(self, iterations, max_rate, start_rate=None,
last_iterations=None, last_rate=None):
self.iterations = iterations
self.max_rate = max_rate
self.start_rate = start_rate or max_rate / 10
self.last_iterations = last_iterations or iterations // 10 + 1
self.half_iteration = (iterations - self.last_iterations) // 2
self.last_rate = last_rate or self.start_rate / 1000
self.iteration = 0
def _interpolate(self, iter1, iter2, rate1, rate2):
return ((rate2 - rate1) * (self.iteration - iter1)
/ (iter2 - iter1) + rate1)
def on_batch_begin(self, batch, logs):
if self.iteration < self.half_iteration:
rate = self._interpolate(0, self.half_iteration, self.start_rate, self.max_rate)
elif self.iteration < 2 * self.half_iteration:
rate = self._interpolate(self.half_iteration, 2 * self.half_iteration,
self.max_rate, self.start_rate)
else:
rate = self._interpolate(2 * self.half_iteration, self.iterations,
self.start_rate, self.last_rate)
rate = max(rate, self.last_rate)
self.iteration += 1
K.set_value(self.model.optimizer.lr, rate)
n_epochs = 25
onecycle = OneCycleScheduler(len(X_train) // batch_size * n_epochs, max_rate=0.05)
history = model.fit(X_train_scaled, y_train, epochs=n_epochs, batch_size=batch_size,
validation_data=(X_valid_scaled, y_valid),
callbacks=[onecycle])
Avoiding Overfitting Through Regularization
$\ell_1$ and $\ell_2$ regularization
layer = keras.layers.Dense(100, activation="elu",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(0.01))
# or l1(0.1) for ℓ1 regularization with a factor or 0.1
# or l1_l2(0.1, 0.01) for both ℓ1 and ℓ2 regularization, with factors 0.1 and 0.01 respectively
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="elu",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(0.01)),
keras.layers.Dense(100, activation="elu",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(0.01)),
keras.layers.Dense(10, activation="softmax",
kernel_regularizer=keras.regularizers.l2(0.01))
])
model.compile(loss="sparse_categorical_crossentropy", optimizer="nadam", metrics=["accuracy"])
n_epochs = 2
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid))
from functools import partial
RegularizedDense = partial(keras.layers.Dense,
activation="elu",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(0.01))
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
RegularizedDense(300),
RegularizedDense(100),
RegularizedDense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy", optimizer="nadam", metrics=["accuracy"])
n_epochs = 2
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid))
Dropout
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(300, activation="elu", kernel_initializer="he_normal"),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal"),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy", optimizer="nadam", metrics=["accuracy"])
n_epochs = 2
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid))
Alpha Dropout
tf.random.set_seed(42)
np.random.seed(42)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.AlphaDropout(rate=0.2),
keras.layers.Dense(300, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.AlphaDropout(rate=0.2),
keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.AlphaDropout(rate=0.2),
keras.layers.Dense(10, activation="softmax")
])
optimizer = keras.optimizers.SGD(lr=0.01, momentum=0.9, nesterov=True)
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer, metrics=["accuracy"])
n_epochs = 20
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid))
model.evaluate(X_test_scaled, y_test)
model.evaluate(X_train_scaled, y_train)
history = model.fit(X_train_scaled, y_train)
MC Dropout
tf.random.set_seed(42)
np.random.seed(42)
y_probas = np.stack([model(X_test_scaled, training=True)
for sample in range(100)])
y_proba = y_probas.mean(axis=0)
y_std = y_probas.std(axis=0)
np.round(model.predict(X_test_scaled[:1]), 2)
np.round(y_probas[:, :1], 2)
np.round(y_proba[:1], 2)
y_std = y_probas.std(axis=0)
np.round(y_std[:1], 2)
y_pred = np.argmax(y_proba, axis=1)
accuracy = np.sum(y_pred == y_test) / len(y_test)
accuracy
class MCDropout(keras.layers.Dropout):
def call(self, inputs):
return super().call(inputs, training=True)
class MCAlphaDropout(keras.layers.AlphaDropout):
def call(self, inputs):
return super().call(inputs, training=True)
tf.random.set_seed(42)
np.random.seed(42)
mc_model = keras.models.Sequential([
MCAlphaDropout(layer.rate) if isinstance(layer, keras.layers.AlphaDropout) else layer
for layer in model.layers
])
mc_model.summary()
optimizer = keras.optimizers.SGD(lr=0.01, momentum=0.9, nesterov=True)
mc_model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer, metrics=["accuracy"])
mc_model.set_weights(model.get_weights())
Now we can use the model with MC Dropout:
np.round(np.mean([mc_model.predict(X_test_scaled[:1]) for sample in range(100)], axis=0), 2)
Max norm
layer = keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal",
kernel_constraint=keras.constraints.max_norm(1.))
MaxNormDense = partial(keras.layers.Dense,
activation="selu", kernel_initializer="lecun_normal",
kernel_constraint=keras.constraints.max_norm(1.))
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
MaxNormDense(300),
MaxNormDense(100),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy", optimizer="nadam", metrics=["accuracy"])
n_epochs = 2
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid))
Exercises
1. to 7.
See appendix A.
8. Deep Learning
8.1.
Exercise: Build a DNN with five hidden layers of 100 neurons each, He initialization, and the ELU activation function.
8.2.
Exercise: Using Adam optimization and early stopping, try training it on MNIST but only on digits 0 to 4, as we will use transfer learning for digits 5 to 9 in the next exercise. You will need a softmax output layer with five neurons, and as always make sure to save checkpoints at regular intervals and save the final model so you can reuse it later.
8.3.
Exercise: Tune the hyperparameters using cross-validation and see what precision you can achieve.
8.4.
Exercise: Now try adding Batch Normalization and compare the learning curves: is it converging faster than before? Does it produce a better model?
8.5.
Exercise: is the model overfitting the training set? Try adding dropout to every layer and try again. Does it help?
9. Transfer learning
9.1.
Exercise: create a new DNN that reuses all the pretrained hidden layers of the previous model, freezes them, and replaces the softmax output layer with a new one.
9.2.
Exercise: train this new DNN on digits 5 to 9, using only 100 images per digit, and time how long it takes. Despite this small number of examples, can you achieve high precision?
9.3.
Exercise: try caching the frozen layers, and train the model again: how much faster is it now?
9.4.
Exercise: try again reusing just four hidden layers instead of five. Can you achieve a higher precision?
9.5.
Exercise: now unfreeze the top two hidden layers and continue training: can you get the model to perform even better?
10. Pretraining on an auxiliary task
In this exercise you will build a DNN that compares two MNIST digit images and predicts whether they represent the same digit or not. Then you will reuse the lower layers of this network to train an MNIST classifier using very little training data.
10.1.
Exercise: Start by building two DNNs (let’s call them DNN A and B), both similar to the one you built earlier but without the output layer: each DNN should have five hidden layers of 100 neurons each, He initialization, and ELU activation. Next, add one more hidden layer with 10 units on top of both DNNs. You should use the keras.layers.concatenate() function to concatenate the outputs of both DNNs, then feed the result to the hidden layer. Finally, add an output layer with a single neuron using the logistic activation function.
10.2.
Exercise: split the MNIST training set in two sets: split #1 should containing 55,000 images, and split #2 should contain contain 5,000 images. Create a function that generates a training batch where each instance is a pair of MNIST images picked from split #1. Half of the training instances should be pairs of images that belong to the same class, while the other half should be images from different classes. For each pair, the training label should be 0 if the images are from the same class, or 1 if they are from different classes.
10.3.
Exercise: train the DNN on this training set. For each image pair, you can simultaneously feed the first image to DNN A and the second image to DNN B. The whole network will gradually learn to tell whether two images belong to the same class or not.
10.4.
Exercise: now create a new DNN by reusing and freezing the hidden layers of DNN A and adding a softmax output layer on top with 10 neurons. Train this network on split #2 and see if you can achieve high performance despite having only 500 images per class.